Forse stiamo già pianificando il viaggio per le vacanze estive, e magari la meta è la Polonia, e poi la Russia è lì vicino. Potremmo andare alla ricerca di una misteriosa città: Konigsberg. Faceva parte della Prussia, vi nacque il grande filosofo e fisico Immanuel Kant.
Cerca, cerca, non la troveremo.
Oggi questa città si chiama Kaliningrad. Dopo la prima guerra m
ondiale la città passò alla Polonia. Nel ’38 Hitler ne reclamò il possesso. Dopo la sconfitta dei nazisti, la città fu assegnata all’Unione Sovietica.
Ma non è per Kant che questa città è rimasta famosa, lo è per un mitico problema logico. Nel ‘700 i ricchi mercanti della città si appassionarono ad una questione senza trovarne una soluzione.
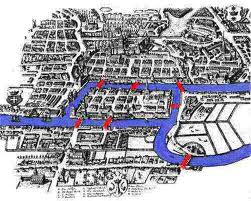Sei ponti congiungono i quartieri della città di Konisberg con due isolette adibite a parco. Un settimo e ultimo ponte collega le isole tra loro. Gli abitanti di Konisberg volevano trovare un modo che consentisse loro di fare una passeggiata che attraversasse tutti e sette i ponti, passando una e una sola volta su ciascuno di essi. Osservando la mappa qui a fianco aiutandosi con una matita si provi a trovare una soluzione…
Tenta, tenta, tenta, (pausa…).
Fu il grande matematico Eulero a dimostrare che non c’erano soluzioni possibili e convinse la popolazione a mettersi il cuore in pace.
Qualcuno andrà sul posto a verificare?
Proviamo ora a cercare un percorso unico più semplice, facendo un gioco che Lewis Carroll (quello di Alice nel paese delle Meraviglie) proponeva ai suoi piccoli amici.
I Cerchi Intrecciati. Passa una e una sola volta su ciascun arco di cerchio:
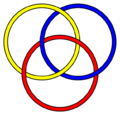
Ancora una volta utilizzare la matita per trovare il percorso. I punti di incrocio sono 6, mentre a Konigsberg erano 7.
Provare per credere! Ricordando che i bimbi, amici di Carroll, ce la facevano facilmente.
E per saperne di più cercare in Internet informazioni su Eulero e i grafi.